HSJA 攻击¶

文章 作者是来自加州大学伯克利分校。

和我们之前做笔记的 FGSM, PGD, C&W 攻击不一样，HSJA 攻击是一种黑盒攻击。但其实本质上和白盒攻击区别没有那么大。

回顾我们之前在 C&W 的动机角度聊过的，一次理想的攻击需要追求两个拮抗的目标：使模型出错（分为有目标和无目标攻击）和扰动尽可能小（肉眼难以发觉）。为此我们将这两个指标量化，第一个目标用 \(f\) 函数指示，第二个目标使用范数约束。最后利用模型的梯度信息进行优化。

现在模型变成黑盒了，拿不到梯度信息了，咋办？

HSJA 提出的方案是：先在决策边界逼近原始图像，然后再利用分类结果重构梯度信息，逐步迭代生成。

二分逼近¶

首先需要明确的是，如果我们对图像做任何扰动之后，标签没有发生任何改变，这就意味着我们不能从中获取任何（梯度）信息。因此我们首先需要做的是把图像移动到决策边界。

假设我们有源图像 \(x^*\)，目标图像 \(x\)，其输出符合我们的需要。如果我们要进行有目标攻击，我们大可以把 \(x\) 设置为我们需要的类别图像；如果是无目标攻击，我们可以倍增加噪直到获取到一个差异的分类。现在我们要基于这两个样本来找到决策边界。

很自然地，我们会使用二分法。我们定义一个指标函数 \(\phi(x_t)\)，为 \(-1\) 代表分为原类别，为 \(1\) 代表分为目标类别。对于 \(\alpha\in (0,1)\)，定义

通过对 \(\alpha\) 做二分法（也就是在 \(L\) 范数下投影到线段中点），就可以在满足 \(L\) 范数精度小于阈值 \(\theta\) 内找到刚刚好使得 \(\phi\) 改变的 \(\hat\alpha\)。

我们将这个流程抽象成一个函数，接受 \(x,x^*,\theta, L\)，分别代表输入图像，目标图像，估计的决策边界宽度（也就是二分阈值）以及约束的范数，最后输出的是 \(\hat x=x(\hat\alpha)\)，和输入目标样本的分类一致但更靠近决策边界。

估计边界梯度¶

类似于 C&W 攻击，我们需要定义一个基于决策的损失函数，通过最优化这个损失函数，来实现成功的攻击。

对于有目标 \(c^\dagger\) 的攻击，我们需要最大化这个类别的 logits 而最小化其他类别的 logits；对于无目标 \(c^*\) 的攻击，我们需要最大化其他类别的 logits 而最小化这个类别的 logits。也就是原文的式 (1)：

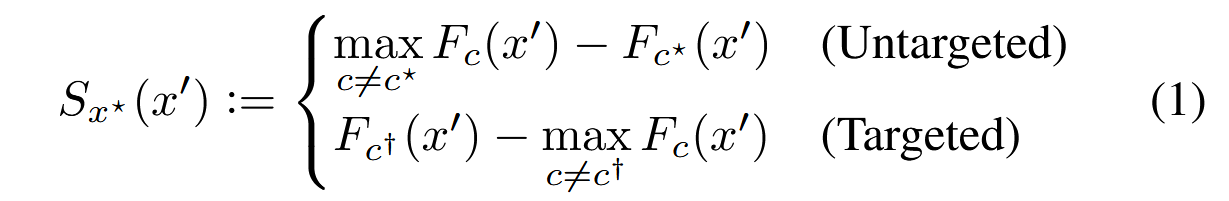
我们的目的就是在 \(S\) 上做梯度上升，而现在的问题是，我们只有样本的分类信息（也就是 \(\phi\) 就是 \(S\) 的符号函数），我们需要基于此估计梯度信息。

现在，基于二分法，我们有了一个在边界的样本 \(\hat x\)，我们可以在上面进行扰动，为此，我们首先生成一个在单位球上均匀分布的样本集合（可以通过正态分布投影到超球面，也可以通过基于拒绝采样的 Marsaglia 算法）得到 \(u_0, \dots, u_B\)，然后我们进行扰动，也就是计算

下面我们要基于此来估计梯度了。首先计算 \(S_i\) 的均值

这表征此样本的一个基线估计，然后我们计算估计的梯度：

这里的 \(B-1\) 就是利用的无偏估计，虽然我觉得用处不大，因为我们马上就要归一化：

迭代求解¶

现在，我们已经在决策边界处获得了一个候选点 \(\hat x\) 以及该点的估计梯度方向 \(v\)，下面我们要根据这些信息进行进一步的迭代求解。

和 PGD 等其他基于梯度的方法类似，我们也进行投影梯度下降，不过这里的梯度是我们估计的梯度 \(v\)。因此现在选择一个参数 \(\xi\) 计算

但是有可能用力过猛飞出目标样本的决策边界了……因此我们要折半 \(\xi\) 使得其保留在原有的边界内。

这个 \(\tilde x\) 就是相对原始的目标样本 \(x\) 更优的目标了（因为我们沿着梯度的方向走了一步），因此，我们持续进行迭代，直到达到最大的次数限制或者已经收敛而不再变化。

最后，为了我们可以再进行一次二分搜索，使得输出 \(\hat x\) 在决策边界上，而更靠近原始样本 \(x^*\)。

其实这个有点类似于 EM 算法这种交替的流程，或者类似于 GAN 的训练。首先通过二分找到靠近决策边界的对抗样本来减少扰动，然后估计梯度来优化对抗样本的分类置信度，如此交替进行。

参数设置与收敛性分析¶

刚刚对算法只是模糊地提点了一下，下面我们来详细讨论一下刚刚算法里面提到的一堆参数的设置，这决定了算法的收敛性。

首先，作者针对基于梯度的一般迭代过程给出了定理一：

这里 \(\xi_t\) 就是往梯度方向移动的步长，离目标越近，时间越久，步长越小，因此用图中的式子进行建模，最后可以得到源图像和对抗样本的余弦相似度可以被 bound 进这个范围内，为了尽可能使得余弦相似度快速收敛，选择 \(q=\dfrac 12\)。于是就有了：

紧接着，作者又约束了估计梯度和真实梯度的相似性，通过这个夹角余弦值衡量：

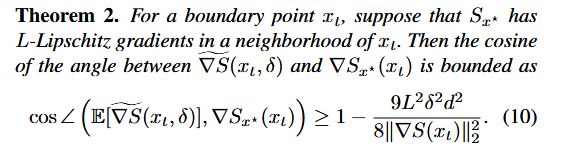
由此，作者要推导 \(\delta\) 和 \(\theta\) 的变化式，我们先来感性理解一下，\(\delta\) 是扰动的探测步长，当我们很接近源图像时，应该更精细地估计梯度，也就是同样带一个 \(\|x_t-x^*\|_p\) 来做保证收敛。

事实上，作者考虑了 \(S_{x^*}(x_t+\delta_t u)\) 在 \(x_t\) 处的泰勒展开，只对一阶项里面，分为原类别的球冠做分析，最后得到落入球冠的概率和 \(c\) 有关，并得到了 \(c\) 的估计：

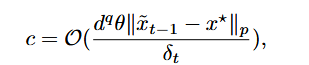
为了让近似误差和维度无关，这个概率要控制在 \(\mathcal O(1)\) 的级别，结合上定理 2 出现的 \((\delta d)^2\)，作者选择

最后，基于定理 3，可以得到梯度估计的方差大概是 \(\mathcal{O}(B^{-2})\)，因此作者选择 \(B_t=B_0\sqrt t\)，能够使得方差以 \(t^{-1}\) 的阶下降。

执行流程¶

基本上要点都理清楚了，下面让 LLM 整理一下流程吧：

初始化¶

• 无目标攻击：从原始样本 \(x^*\) 开始，通过添加均匀随机噪声生成初始样本 \(x_0\) ，使得 \(\phi_{x^*}(x_0) = 1\) （即模型误分类）。
• 有目标攻击：从测试集中随机选择一个属于目标类别的样本作为初始点 \(x_0\) ，使得 \(\phi_{x^*}(x_0) = 1\) 。
• 设置初始批量大小 \(B = 100\) ，并随迭代次数 \(t\) 以 \(\sqrt{t}\) 速率增加，以降低方差。

迭代过程（对于每个迭代 \(t = 0, 1, 2, \ldots\) ）¶

直到达到最大查询次数 \(T\) 或收敛，执行以下步骤：

步骤A: 边界搜索（Binary Search）¶

• 目的：将当前点 \(x_t\) 精确地投影到决策边界上，确保 \(\phi_{x^*}(x_t) = 1\) 。
• 使用算法1（Bin-Search）：
• 输入：当前点 \(x_t\) 和原始点 \(x^*\) ，其中 \(\phi_{x^*}(x_t) = 1\) ， \(\phi_{x^*}(x^*) = -1\)。
• 过程：
  • 设置 \(\alpha_l = 0\) ， \(\alpha_u = 1\) 。
  • 当 \(|\alpha_u - \alpha_l| > \theta\) （阈值设为 \(\theta = d^{-q-1}\) ，其中 \(q = 1 - 1/p\) ）时：
  • 计算中点 \(\alpha_m = (\alpha_l + \alpha_u)/2\) 。
  • 计算投影点 \(x_m = \Pi_{x^*, \alpha_m}(x_t)\) （根据距离度量选择投影方式）。
  • 如果 \(\phi_{x^*}(x_m) = 1\) ，则更新 \(\alpha_u = \alpha_m\) ；否则更新 \(\alpha_l = \alpha_m\) 。
  • 输出投影点 \(x_t' = \Pi_{x^*, \alpha_u}(x_t)\) ，作为新的边界点。

步骤B: 梯度方向估计¶

• 目的：在边界点 \(x_t\) 处估计梯度方向 \(\nabla S_{x^*}(x_t)\) 。
• 使用蒙特卡洛估计：
• 生成 \(B\) 个随机向量 \(\{u_b\}_{b=1}^B\) ，服从单位球面上的均匀分布。

• 计算梯度估计：

  \[ \widehat{\nabla S}(x_t, \delta_t) = \frac{1}{B-1} \sum_{b=1}^{B} \left( \phi_{x^*}(x_t + \delta_t u_b) - \overline{\phi_{x^*}} \right) u_b \]

  其中， \(\overline{\phi_{x^*}} = \frac{1}{B} \sum_{b=1}^{B} \phi_{x^*}(x_t + \delta_t u_b)\) 是基线，用于减少方差。 - 扰动大小 \(\delta_t\) 的选择：

  \[ \delta_t = d^{-1} \| \tilde{x}_{t-1} - x^* \|_p \]

  其中 \(d\) 是输入维度， \(p\) 是距离范数。

步骤C: 步长搜索（Geometric Progression）¶

• 目的：确定沿梯度方向的步长，使得更新后的样本仍处于目标侧。
• 计算更新方向：
• 对于ℓ₂攻击： \(v_t = \widehat{\nabla S}(x_t, \delta_t) / \| \widehat{\nabla S}(x_t, \delta_t) \|_2\)
• 对于ℓ∞攻击： \(v_t = \text{sign}(\widehat{\nabla S}(x_t, \delta_t))\)
• 初始步长： \(\xi_t = \| x_t - x^* \|_p / \sqrt{t}\) （基于Theorem 1的理论建议）。
• 通过几何级数调整步长：
• 计算候选点： \(\tilde{x}_t = x_t + \xi_t v_t\)
• 如果 \(\phi_{x^*}(\tilde{x}_t) = -1\) ，则将步长减半（ \(\xi_t \leftarrow \xi_t / 2\) ），重复直到 \(\phi_{x^*}(\tilde{x}_t) = 1\) 。

步骤D: 投影回边界¶

• 目的：将更新后的点 \(\tilde{x}_t\) 投影回决策边界，得到下一迭代点 \(x_{t+1}\) 。
• 使用算法1（Bin-Search），输入为 \(\tilde{x}_t\) 和 \(x^*\) ，输出投影点 \(x_{t+1}\) 。
• 投影方式取决于距离度量：
• ℓ₂投影： \(\Pi_{x^*, \alpha_t}^2(\tilde{x}_t) = \alpha_t x^* + (1 - \alpha_t) \tilde{x}_t\)
• ℓ∞投影：对每个像素裁剪到区间 \([x_i^* - c, x_i^* + c]\) ，其中 \(c = \alpha_t \| \tilde{x}_t - x^* \|_\infty\)

1
2
3
4
5
6
7

@online{hsja,
    title={HSJA 攻击},
    author={Yan Li},
    year={2025},
    month={Sep},
    url={\url{https://dicaeopolis.github.io/DNN/model-attack/hsja}},
}